Image Processing with Optimally Designed Parabolic Partial Differential Equations
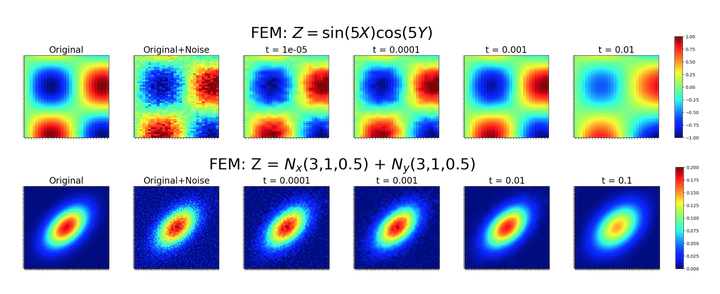 Image credit: Qiuyi Wu
Image credit: Qiuyi WuOngoing Thesis Project
Discovering underlying patterns and trajectories from limited and noisy data is a central problem in machine learning. In the world of computer vision and image processing, the current cutting-edge deep generative models such as GAN, VAE, and diffusion models have achieved great success in a wide variety of data modalities. Yet no matter how advanced the generative models are, they can all benefit from high-quality input data with high signal-to-noise ratio, and thus help offset their limitations of unstable training and expensive computation. Smoothing is one of the most common methods to increase signal-to-noise ratio and enhance subsequent analyses. However, traditional kernel smoothing methods suffer from lack of adaptivity and the curse of dimensionality; the accuracy and efficiency typically worsen exponentially in high dimensional settings.
In my doctoral thesis work, I propose an adaptive General Kernel Smoothing-Finite Element Method (GKS-FEM), that leverages the equivalence between the GKS and the general second order parabolic partial differential equation (PDE), the latter of which I discretize using the finite element method (FEM) to obtain numerical smoothing schemes which are fast and robust in high dimension. Nevertheless, the underlying function is rarely available in real life. Hence, instead of relying on prior information or assuming a functional form, I let the data speak for itself and extend the method by replacing deterministic functions by random functions. Moreover, by using a mixed-effects modeling technique, I can more effectively borrow information across subjects. Furthermore, population-level information about random functions can be learned from a large set of training data once, so that individual users do not have to repeat this time-consuming task.
From a broader perspective, I attempt to bridge the gap between mathematics and statistics by applying mathematical techniques in novel ways to solve statistical problems. I have developed a kernel smoothing-finite element method (FEM), which applies the FEM method for discretizing partial differential equations to kernel smoothing tasks. The method is designed to ensure efficiency and stability in high-dimensional scenarios. The primary applications for this work are in image processing and denoising tasks, which play an essential role in neuroimaging studies.